booleana

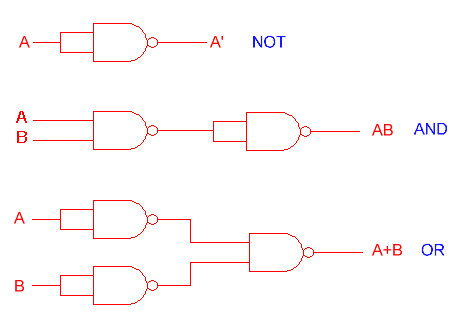
Para probar que podemos construir cualquier función booleana utilizando sólo compuertas NAND, necesitamos demostrar cómo construir un inversor (NOT), una compuerta AND y una compuerta OR a partir de una compuerta NAND, ya que como se dijo, es posible implementar cualquier función booleana utilizando sólo los operadores booleanos AND, OR y NOT. Para construir un inversor simplemente conectamos juntas las dos entradas de una compuerta NAND. Una vez que tenemos un inversor, construir una compuerta AND es fácil, sólo invertimos la salida de una compuerta NAND, después de todo, NOT ( NOT (A AND B)) es equivalente a A AND B. Por supuesto, se requieren dos compuertas NAND para construir una sola compuerta AND, nadie ha dicho que los circuitos implementados sólo utilizando compuertas NAND sean lo óptimo, solo se ha dicho que es posible hacerlo. La otra compuerta que necesitamos sintetizar es la compuerta lógica OR, ésto es sencillo si utilizamos los teoremas de DeMorgan, que en síntesis se logra en tres pasos, primero se reemplazan todos los "·" por "+" después se invierte cada literal y por último se niega la totalidad de la expresión:

A OR B
A AND B.......................Primer paso para aplicar el teorema de DeMorgan
A' AND B'.....................Segundo paso para aplicar el teorema de DeMorgan
(A' AND B')'..................Tercer paso para aplicar el teorema de DeMorgan
(A' AND B')' = A' NAND B'.....Definición de OR utilizando NAND

Gráficamente podemos representar las operaciones ejecutadas de la siguiente manera:

Algebra booleana

La relación que existe entre la lógica booleana y los sistemas de cómputo es fuerte, de hecho se dá una relación uno a uno entre las funciones booleanas y los circuitos electrónicos de compuertas digitales. Para cada función booleana es posible diseñar un circuito electrónico y viceversa, como las funciones booleanas solo requiren de los operadores AND, OR y NOT podemos construir nuestros circuitos utilizando exclusivamente éstos operadores utilizando las compuertas lógicas homónimas:

Unidad4

 

PROFESOR: FIDELIO CASTILLO ROMERO

 

ALUMNOS: JORGE ALFONSO RUIZ FLORES

HUGO ALBERTO REYES DE LA CRUZ

HUGO ARMANDO ACOPA LOPEZ

HIPOLITO SOSA MARTINEZ

JOSE CARLOS SANCHEZ SANCHEZ

GENRY SASTRE GARCIA

CARRERA: ING. EN SISTEMAS COMPUTACIONALES

 

MATERIA: MATEMATICAS PARA COMPUTACION

 

SEMESTRE: 1

 

GRUPO: B

 

 

 

 

         VILLAHERMOSA, TAB. 31 DE MAYO DEL 2010

 

 

Camino de Euler.
Es aquel camino que recorre todos los nodos pasando por todas las aristas solamente una vez. Una característica importante de los grafos que tienen camino de Euler es que siempre comienzan y terminan en nodos que terminan en valencia impar.

Circuito de Euler.
Es aquel ciclo que recorre todos los nodos pasando por todos las aristas solamente una vez.
Un grafo tiene un Circuito de Euler si y solo si es conexo y todos sus nodos tienen valencia par.

 

 

En matemáticas y ciencias de la computación, un grafo (del griego grafos: dibujo, imagen) o gráfica es el principal objeto de estudio de la teoría de grafos.

Informalmente, un grafo es un conjunto de objetos llamados vértices o nodos unidos por enlaces llamados aristas o arcos, que permiten representar relaciones binarias entre elementos de un conjunto.

Típicamente, un grafo se representa gráficamente como un conjunto de puntos (vértices o nodos) unidos por líneas (aristas).

Desde un punto de vista práctico, los grafos permiten estudiar las interrelaciones entre unidades que interactúan unas con otras. Por ejemplo, una red de computadoras puede representarse y estudiarse mediante un grafo, en el cual los vértices representan terminales y las aristas representan conexiones (las cuales, a su vez, pueden ser cables o conexiones inalámbricas).

Prácticamente cualquier problema puede representarse mediante un grafo, y su estudio trasciende a las diversas áreas de las ciencias exactas y las ciencias sociales.

 

          hacer las siguientes conversiones:

        53710---->__2 =100011001

        1653210---->____2=10000010010100

        101012------->____10=1+4+16=21

        11100111---->___10=1+2+4+32+64+118=231